PerCycleValue

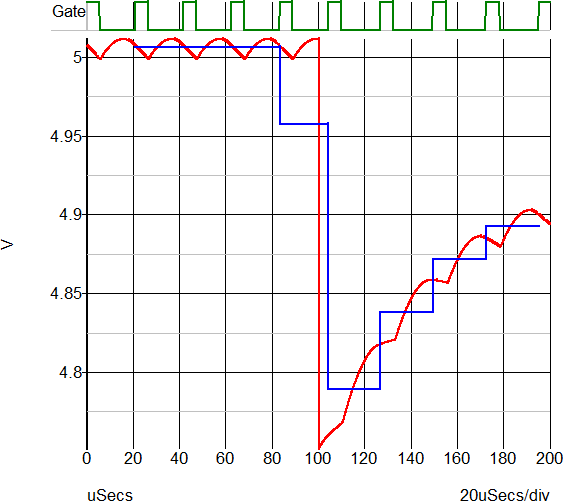
Processes the input vector measuring Minimum, Maximum, Mean, Peak-to-Peak, or the RMS value of the input vector during time intervals generated by the timing vector. The returned vector contains the measured value of the input vector, such as the Mean value, plotted against the timing vector x-axis value, for example, time. The return vector is either "stepped" or smooth. A stepped return vector will have vertical discontinuities at the beginning and end of timing vector period. A smooth return vector will have a single data point per input vector period, located at the mid-point of the input vector period.

Argument 4 specifies the output curve type with the default being "stepped". The stepped return vector will change value only at the edges detected in the input vector. The value will be constant during the entire period. A smooth input vector will have a single data point at the mid-point of the input vector period. The points will be connected resulting in a smooth curve from one period to the next.

Argument 5 specifies edge direction. If set to 0 either direction will be accepted. If set to 1 only positive edges will be detected and if set to -1 only negative edges will be detected. This argument is only used for the period and frequency measurements. All other measurements will be processed with the Direction argument set to 1, indicating positive edges.

Arguments

Argument 1

The vector to measure the Minimum, Maximum, Mean, Peak-to-Peak, or the RMS values for. The function finds the timing periods based on the timing vector passed as the second argument.

Argument 2

The vector to determine the period information for the vector input in the first argument. It is expected that the vector input to the first argument will contain noise which precludes using the first argument for any timing measurements. to fail. For this reason, the function finds the edges from this vector using a threshold of $\frac{maximum+minimum}{2}$. For this reason, it is important that the vector have a uniform amplitude and is noise-free around the trigger threshold.

It is possible that the input vector is free of noise, in which case the same vector could be input to both the first and second function arguments. An example of this would be the output of a gate which has well-defined transitions and uniform maximum and minimum amplitudes.

Argument 3

A pre-defined measurement function to make, one of:

• minimum
• maximum
• mean
• peak-to-peak
• rms

Argument 4

Determines the type of return curve, one of:

• stepped
• smooth

Argument 5

Determines the edges used to process the timing vector, one of:

• -1: Falling edges
• 1 : Rising edges
• 0 : Both Rising and Falling Edges

Returns

Return type: real array

A real vector of the measured values from the input vector, with reference values taken from the timing vector according to the fourth argument. The return vector is formatted to be plotted directly on the waveform viewer.

Example

A call to: