Advanced SIMPLIS Training
|
To download the examples for Module 3, click Module_3_Examples.zip
In this Topic Hide
How to setup a SIMPLIS Monte Carlo Analysis.
How to apply the Gauss(), Unif(), and Wc() probability distribution functions to vary component values.
How to match the percentage variation of two or more component values.
How multiple processor cores can be used to reduce the time required to execute a Monte Carlo simulation.
How to plot histograms.
How Monte Carlo Seeds are generated.
How to find the seed number for a simulation and how you can repeat a simulation with a known seed number.
Open the schematic 3.1_SelfOscillatingConverter_POP.sxsch.
From the schematic menu, select Monte
Carlo Setup Monte Carlo...
Result: The Define SIMPLIS Multi-Step Analysis
dialog opens. This is the same dialog used to setup the SIMPLIS Multi
Step Analysis; however, the configuration file name is different,
allowing you to save both Multi-Step and a Monte Carlo analysis configuration
information.

Click Run.
Result: The SIMPLIS Monte Carlo Analysis
executes and the graph viewer opens with the curves from the 8 Monte
Carlo steps:
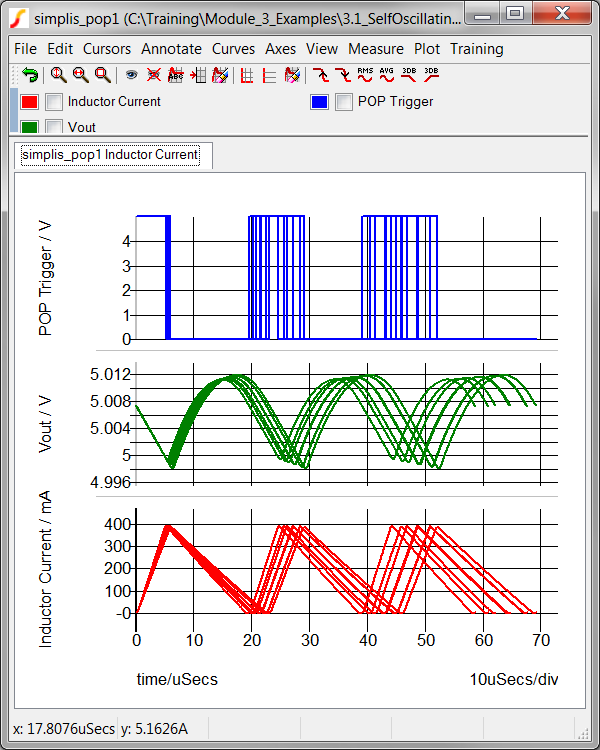
The SIMPLIS Monte Carlo Analysis is similar to the SIMPLIS Mutli-Step Analysis except instead of stepping a parameter, the Monte Carlo seed value is stepped. The seed value is used to determine the values of each statistical distribution function used in the design. If no statistical distribution functions are used in the circuit, each seed value will produce the same simulation results.
There are three statistical distribution functions for use in the SIMPLIS Monte Carlo Analysis, Gauss(), Unif(), and Wc(). Each of these functions has a different numerical return value when the function is called. The table and histograms pictured below describe each function. The histograms were generated with tol=0.1, or 10%, a mean value of 1, with 10,000 steps (runs), and 50 histogram bins.
| Function | Meaning | Histogram |
| Gauss(tol) | Returns a random with a mean of 1.0 and a standard deviation of tol/3. Random values have a Gaussian or Normal distribution. Note: The Gauss() function can return values greater than (1 + tol) and less than (1 - tol). This becomes particularly important when you are using a large tolerance, as the return value may be outside of a reasonable range |
 |
| Unif(tol) | Returns a random value in the range 1.0 +/- tol with a uniform distribution. |
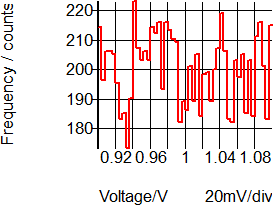 |
| WC(tol) | Returns either 1.0-tol or 1.0+tol chosen at random. |
 |
You assign statistical distribution functions to component values like any other parametrized value. The statistical distribution function and the nominal value must be enclosed in the curly braces {}, indicating the value is an expression to be evaluated. For example, a 1k ohm, 5% resistor with a Gaussian distribution would have the value of:
{1k*Gauss(0.05)}
Every Monte Carlo step, the Gauss(0.05) function will return a value with a Gaussian distribution, which is then multiplied by the nominal value and the resistor is assigned this numerical result. On voltage sources and a few other dialogs, you must use the literal property editing dialog to enter text values enclosed in curly braces. In the next exercise you will edit the value of the input voltage source, V1 using the literal property editing method.
Select the input voltage source V1.
Result: The symbol changes from red to
blue indicating the symbol is selected.
Execute the keyboard shortcut Shift+F7.
Result: The literal parameter value editing
dialog opens:
Enter the uniform distribution: {310*Unif(0.0333)}
Result: The configured dialog should appear
as follows:

Click Ok.
Result: The property value for the input
voltage changes to the uniform distribution of 310V +/- 3.33%.

From the schematic menu, select Monte
Carlo Run Monte Carlo.
Result: The SIMPLIS Monte Carlo Analysis
executes and the graph viewer opens with the curves from the original
8 steps with a constant Input voltage, and the additional 8 steps
from the second Monte Carlo Analysis with input voltage variation.
With the input voltage variation included, the variation of the frequency
of the converter increases significantly.

There are times when you may want to have multiple component values which match or track each other. In the SIMPLIS Monte Carlo analysis, this is accomplished by first assigning a variable statement to depend on a statistical distribution function, then using that variable to parametrize the individual matching components. This "master" variable is evaluated once - from then on, the value is constant.
One place where this comes in useful is for PWL inductors, such as L4 in this example circuit. This inductor is used to model the magnetizing inductance of the transformer including saturation effects. In the next exercise you will verify that the inductance of each segment of the inductor L4 is varied in proportion to a Gaussian distribution function.
Double click on L4.
Result: The Define PWL Inductor: L4 dialog
opens:
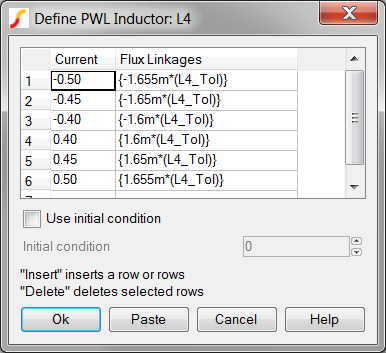
Note that each Flux Linkage value is multiplied by a constant value L4_Tol. Since the Flux Linkage values are the "y-axis" values, and the slope of each PWL segment represents the inductance of that segment, every PWL segment changes inductance by the same percentage.
Click Cancel on the Define PWL Inductor: L4 dialog.
Press F11 to open the command (F11) window. Scroll down to where the L4_Tol is defined:
.var L4_Tol={Gauss(0.20)}
{ '*' }
{ '*' } L4's tolerance : {L4_Tol}
{ '*' }
As you did in section 3.0.2
What Actual Device is Simulated in SIMPLIS?, you look in the deck
file to ascertain exactly what values are used for L4_Tol,
and the PWL inductor L4. From the
command shell menu, select SIMPLIS
Edit Netlist (after preprocess).
Result: the SIMPLIS Deck file opens in Notepad++.
Search for the L4's tolerance comment line:
Use the shortcut key Ctrl+F to open the search dialog.
Type L4's.
Click on the Find Next
button.
Result: The deck file scrolls to line # 12 where the debug
comment is located:

Finally, search for the actual L4 device instantiation line:
Use the shortcut key Ctrl+F to open the search dialog.
Type !L$L4.
Click on the Find Next
button three
times.
Result: The deck file scrolls to line # 49 where the L4
instantiation and its .MODEL line are located:

Piecewise Linear Inductors, such as L4 in this example, are implemented with a .MODEL statement, which in this case, starts on line #50. The PWL points are listed as X,Y pairs starting at X0 and Y0. Notice the X values have the same numerical values you saw in the dialog. The Y-values are all multiplied by the constant value L4_Tol. The L4_Tol is constant because the value is evaluated once per Monte Carlo run, and from that point onwards, the same constant value is used in the expressions for L4_Tol. The value of L4_Tol will almost certainly be different for the next Monte Carlo simulation step.
The value of the L4_Tol variable is 1.01391910298956, which represents a 1.39% increase in inductance values. Calculating the change in inductance is left as an independent study exercise.
As with the SIMPLIS_Multi Step Analysis the SIMetrix/SIMPLIS Pro and Elite licenses can use multiple processor cores to simulate the Monte Carlo steps in parallel. Using multiple cores allows multiple step values to be simultaneously simulated, and the simulation time to be reduced. The number of cores allowed by the licenses are:
| License | Number of Physical Cores |
| Pro | 4 |
| Elite | 16 |
In addition to the maximum number of cores allowed by your license, you are obviously limited by the number of cores your computer has. For this limitation, SIMetrix/SIMPLIS only uses the physical cores, not the hyper-threaded cores. In the next exercise you will run a multi-core, multi-step simulation.
This exercise assumes your computer has more than one physical core and that you are using a SIMetrix/SIMPLIS Pro license.
Close the graph viewer.
From the schematic menu, select Monte
Carlo Setup Monte Carlo...
Result: The Define SIMPLIS Multi-Step Analysis
dialog opens with the Monte Carlo configuration information.

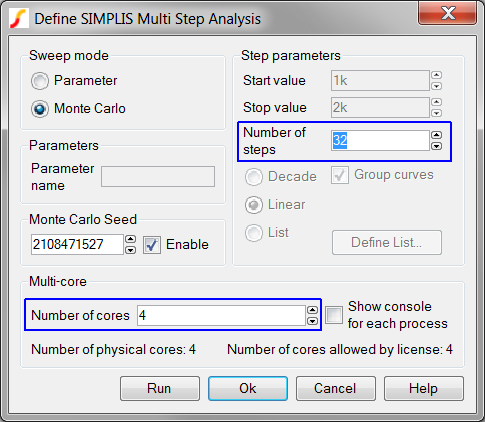
Change the Number of cores to 4, the maximum allowed by the Pro license.
Note: if your machine has either a single core or two cores, the dialog will limit your Number of cores entry. If you have a single core, you can skip this exercise.
Change the Number of steps
to 32.
Result: The configured dialog will appear
as follows:
Click Run.
Result: The Monte Carlo simulation runs
32 steps on the maximum number of physical cores.
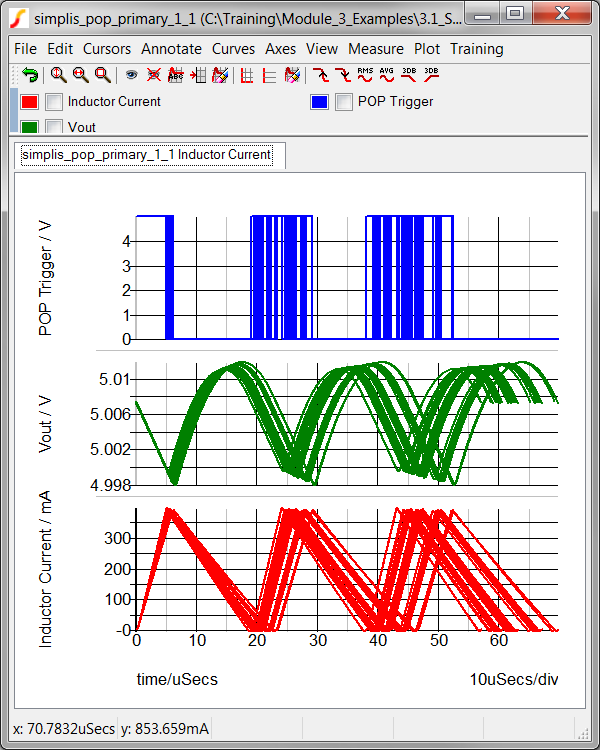
SIMetrix/SIMPLIS has an extremely powerful histogram plotting function. In the last exercise, you executed 32 simulations to get a valid statistical sample, and the histogram plotting functions requires a minimum of 16 runs. In the next two exercises you will plot the histogram for the converter switching frequency.
Before you plot the switching frequency histogram, you'll want to define
the number of bins for the histogram function. The default number of bins
will result in a histogram with too few bins, as the number of bins is
low for a 32 run Monte Carlo Analysis. The default number of bins is:
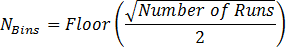
For your 32 run Monte Carlo, this results in only 2 bins! To set the number of bins to 10:
Use the keyboard shortcut Ctrl+C to copy the following text to the windows clipboard:
Set MCNumberOfBins=10
At the SIMetrix/SIMPLIS command shell window, click the mouse in
the command line. The command line is the text entry field
and the Ok button shown in the blue box below:
Result: The keyboard focus is set to the
SIMetrix/SIMPLIS command line interpreter, ready for you to paste
the option setting.
Press Ctrl+V to paste the
option.
Result: The command shell should appear
exactly as follows:
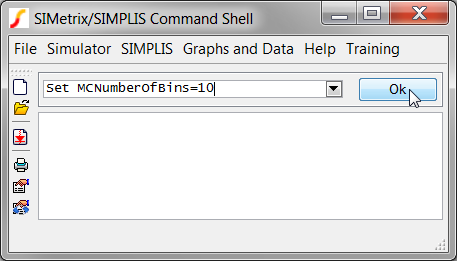
Click the Ok Button.
Result: There is no response from the program,
but the option for the number of Histogram bins has been saved. The
program will use this number of bins until you issue a Unset command,
or change the option to a new value. The Unset command is:
UnSet MCNumberOfBins
Plotting histograms is different from plotting time domain curves because the histogram function is expecting a single measured value per Monte Carlo step. Compare this to plotting the converter output voltage after a transient simulation - there may be 10,000 points in the output voltage vector, each one representing the voltage at a particular simulation time. If you were to average the output voltage over the simulation time span, you would have just one measurement per Monte Carlo step. This is exactly what a histogram is - the frequency of a particular scalar measurement over a statistical sample.
Therefore, every histogram will require a function to operate on the voltage or current, and this function must return a single scalar value for each Monte Carlo step. For the above mentioned example, the function used to return the average value of a voltage or current from a time-domain simulation is Mean1(). For this example you will plot the frequency of the converter frequency using the Frequency() function.
From the schematic menu, select Monte
Carlo Plot Histogram.
Result: The Define Performance Analysis
dialog opens:
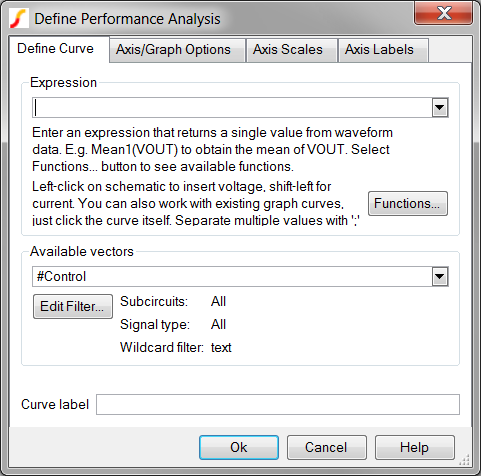
In the Expression field,
type Frequency( and
leave the cursor positioned immediately after the opening parentheses.
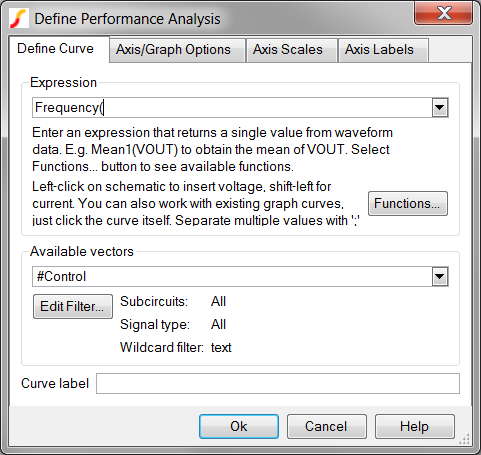
Result: The configured dialog should appear
as follows. Note the cursor is placed immediately after the opening
parentheses. The position of the cursor is important for the next
step!
On the schematic, move the mouse over to the output of the POP
Trigger schematic device.

Click the left mouse button once.
Result: The POP Trigger output net, :33,
is copied to the Define Performance Analysis dialog:
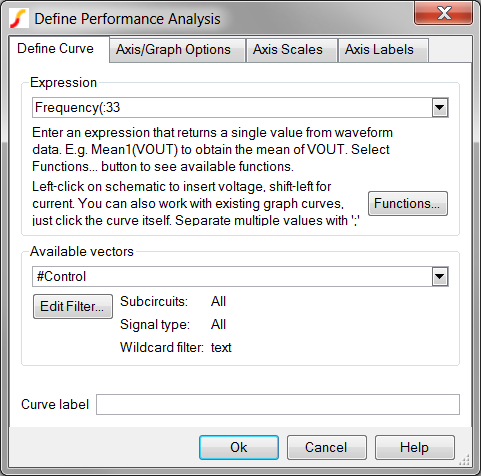
Type a closing parenthesis ).
Result: The final configured dialog should
appear as follows: The final expression is Frequency(:33).

Click Ok.
Result: The histogram for the frequency
of the converter is output to the graph viewer:
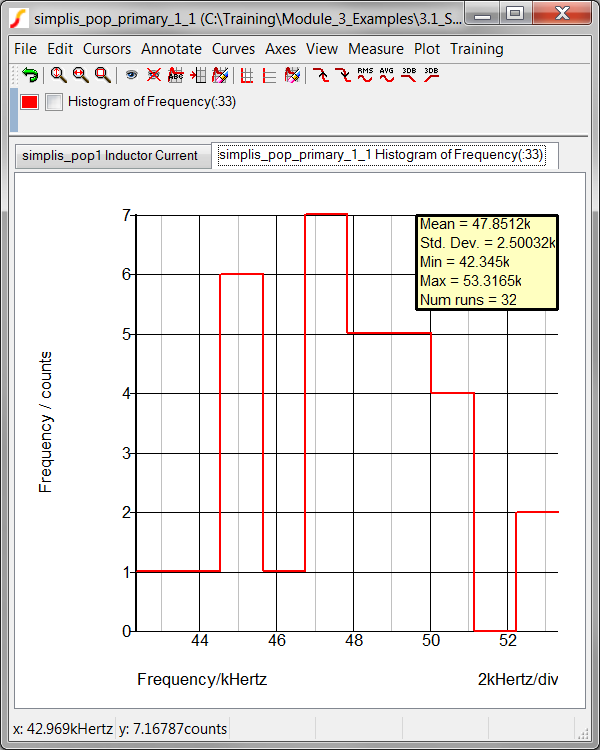
The Define Performance Analysis dialog remembers previously plotted
expressions. If you execute the schematic menu Monte
Carlo Plot Histogram, you can access the previous expressions
with the pull down menu as depicted below. This will save you time
if you wish to re-plot a histogram.

A list of functions which can be used to define the histogram expression is available by clicking on the Functions... button.
More information on using this dialog to generate plots is available by clicking on the Help button.
Behind the scenes, a pseudo-random number generator is used to generate the Monte Carlo seed values. The seed values are used by each statistical probability function to generate the function return value. As a result, a particular Monte Carlo step can be repeated if you know the seed number used for that step, and the circuit has not changed at all between the first and second runs.
In the next exercise you will find the run with the lowest frequency and it's seed number, then repeat a simulation using the seed value.
On the graph viewer window:
Select the transient waveform tab if the histogram is the current tab.
Zoom into the lower right hand corner as shown below:
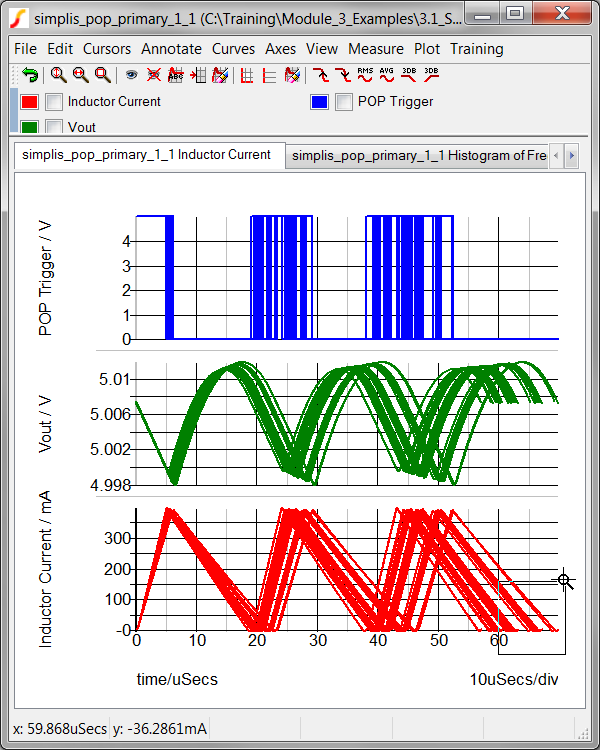
Result: the graph viewer should appear
approximately as follows:

Press the keyboard shortcut C
to turn on the cursors.
Result: A hint box may open, you may click
on the Close button to dismiss it.
Result: The cursors are displayed on the
graph in the lower left corner.
Move your mouse over the cursors until the cursor changes shape
to a 4-way arrow as shown below.
Press and hold the left mouse button while moving the mouse to the right-hand most curve.
Release the mouse button.
Result: The cursor snaps to the nearest
curve.

In the previous step, you moved either the "A"
or the "REF" cursor.
The cursor pictured above is the "A"
cursor, and is the cursor the program uses to read the curve information.
If you moved the "REF"
cursor, repeat for the process for the "A"
cursor. The exact cursor location on the curve is not important.
What is important is the "A"
cursor is on the right-hand most curve which is the step with the
lowest frequency.
Result: The graph viewer now appears as
follows:

From the graph menu, select Cursors
Show Curve Information.
Result: the curve information, including
the Monte Carlo run number is output to the SIMetrix/SIMPLIS command
shell:
Curve name: Inductor
Current (simplis_pop_primary_1_1)
Source group: simplis_pop_primary_1_1
Curve id : 17
Run number : 32
You now know that run number 32 produced the lowest switching frequency. To find the seed value which corresponds to this run number, you need to open the simplis_mclog.log file, which is located in the schematic directory. To open the simplis_mclog.log file,
Right click on the schematic tab:

Select the Open Containing
Folder menu option.
Result: a Windows Explorer window opens
to the schematic directory.
Open the simplis_mclog.log
file in Notepad++ using the context menu:

Result: The simplis_mclog.log file opens
in Notepad++. This file contains all the seed values for the last
Monte Carlo run.

Copy the seed value to the windows clipboard with the keyboard shortcut Ctrl+C.
From the schematic menu, select Monte
Carlo Setup Monte Carlo...
Result: The Define SIMPLIS Multi-Step Analysis
dialog opens with the Monte Carlo configuration information.

Make three changes to the dialog values:
In the Monte Carlo Seed field, paste the seed value: 1152753089
Change the Number of steps to: 1
Change the Number of cores
to: 1
Result: The configured dialog should
appear as follows:
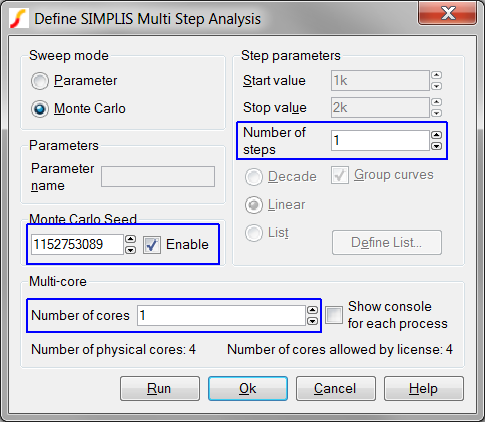
Click Run to run the
known seed.
Result: A single Monte Carlo Step is run,
reproducing the Monte Carlo run with the lowest frequency:
Press the Home key on
the keyboard to zoom the graph viewer to see the full waveforms:

Setting up a SIMPLIS Monte Carlo Analysis is similar to a SIMPLIS Multi-Step Analysis; however, instead of stepping a parameter, the Seed value is stepped.
The Gauss(), Unif(), and Wc() probability distribution functions allow you to vary parameters during a Monte Carlo Analysis.
Matched parameters can be defined by first defining a master variable in the command (F11) window.
Histograms are easily plotted using the schematic menu: Monte Carlo Plot Histogram...
The Seed values used for a SIMPLIS Monte Carlo Analysis are saved to the simplis_mclog.log file.
Any single seed value can be simulated to reproduce a run with unusual or otherwise interesting results.
© 2015 simplistechnologies.com | All Rights Reserved