1.0.6 AC Analysis
The SIMPLIS AC analysis analyzes the small signal response of a circuit at the operating point found in the 1.0.5 POP Analysis. This is analogous to SPICE simulators, which finds an AC analysis around a DC operating point. Switching power converters don't have a DC operating point, so the SPICE AC analysis cannot be used on a time-domain switching power converter.
In this topic:
Key Concepts
This topic addresses the following key concepts:
- The SIMPLIS AC Analysis is a time-domain analysis.
- The AC analysis results are valid at the switching operating point found in the POP analysis.
What You Will Learn
In this topic, you will learn the following:
- How SIMPLIS simulates the AC response of a time domain model.
- The difference between the AC results on a time-domain model and an averaged model.
Getting Started: Running an AC Analysis
- If the waveform viewer is open, close it.
- Open the schematic titled 1.2_SIMPLIS_tutorial_buck_converter.sxsch.
- From the menu bar select .
- Un-check all analysis check boxes, and check the AC analysis checkbox. Result: The POP Checkbox is also checked, but disabled - indicating you must run a POP analysis before every AC analysis.
- The dialog should appear as follows:
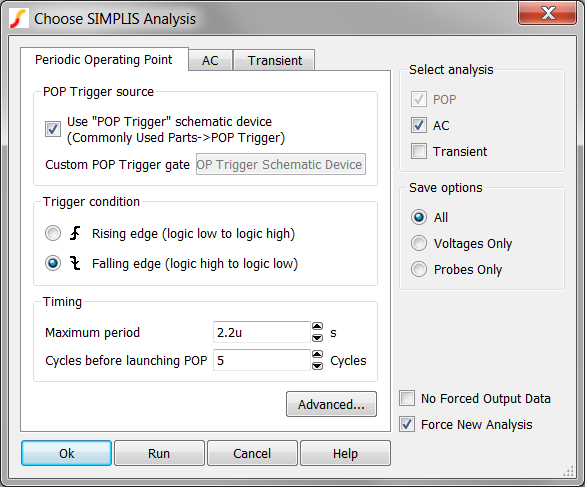
- Click Run. Result: SIMPLIS runs a POP analysis followed by an AC analysis on the Self Oscillating Converter. As with the last section, the waveform viewer opens with 3 switching cycles of data, but also with the AC response of the control loop.
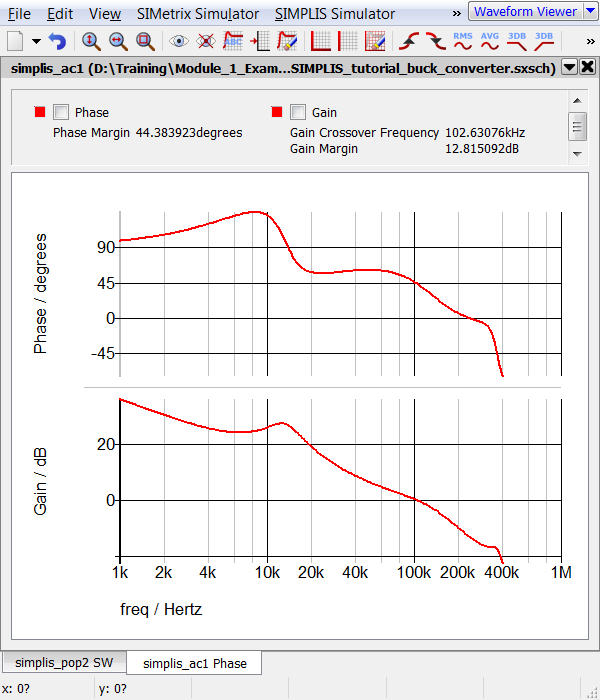
Discussion
When you go into the lab and connect your switching power system to a network analyzer, you are measuring the AC response of the circuit in the time domain. Your circuit doesn't suddenly change to a averaged small signal model when the network analyzer is connected to it. The SIMPLIS AC analysis works exactly in the same way; it performs an AC analysis on a time-domain simulation model.
How the SIMPLIS AC Analysis works
- You run a POP analysis on the circuit. This analysis finds the large signal steady state operating point of the circuit.
- You run an AC analysis on the circuit using the POP analysis as the operating
point. For each frequency in the sweep, the AC analysis does the following:
- Sets all AC sources (for AC analysis) to a common frequency - the analysis, or perturbation, frequency. The analysis frequency is not the switching frequency where the POP analysis took place - it is the frequency where the small signal analysis is run.
- These AC sources are time-domain sinusoidal, and the amplitudes of each source is set to an infinitesimally small number.
- SIMPLIS simulates the time domain response of the circuit to the AC perturbation.
- Using Fourier methods, SIMPLIS extracts the small signal response of the circuit from the time-domain data.
During an AC sweep, steps a-d above are repeated for each frequency in the sweep. The circuit is perturbed by a single frequency, and that frequency is stepped.
What Can Go Wrong?
- If the circuit does not POP successfully, in other words, if SIMPLIS cannot find a stable steady-state periodic operating point, the AC analysis will not be run. A warning message appears in the command shell.
- Your circuit may converge during the POP analysis, but to a periodic operating point which you are not expecting. A common example occurs when the POP analysis results in the circuit operating in a current limit or other fault condition. Since during current limit operation, the voltage loop is essentially open, the gain of the voltage loop is greatly attenuated compared to what it would be in normal operation..
Conclusions and Key Points to Remember
- The SIMPLIS AC analysis works just like a network analyzer in the lab.
- Every AC analysis must be preceded by a POP analysis.
- The AC results are totally and completely dependent on the operating point found during the POP analysis.
- The AC analysis is performed on the time domain model - including all ripple effects.
- Since a small signal averaged model is not required, design time is reduced and only one time-domain model is required.