Current Controlled Current Source

In this topic:

Netlist Entry

Linear Source

Fxxxx nout+ nout- vc current_gain
nout+ Positive output node
nout- Negative output node
vc Controlling voltage source
current_gain Output current/Input current
SPICE2 polynomial sources are also supported in order to maintain compatibility with commercially available libraries for IC's. (Most operational amplifier models for example use several polynomial sources). In general, however the arbitrary source (see Arbitrary Source) is more flexible and easier to use.

Polynomial Source

Fxxxx nout+ nout- POLY( num_inputs ) vc1 vc2 ...
+ polynomial_specification
vc1, vc2 Controlling voltage sources
num_inputs Number of controlling currents for source.
polynomial_specification See Polynomial Specification.

The specification of the controlling voltage source or source requires additional netlist lines. The schematic netlister automatically generates these for the four terminal device supplied in the symbol library.

Example

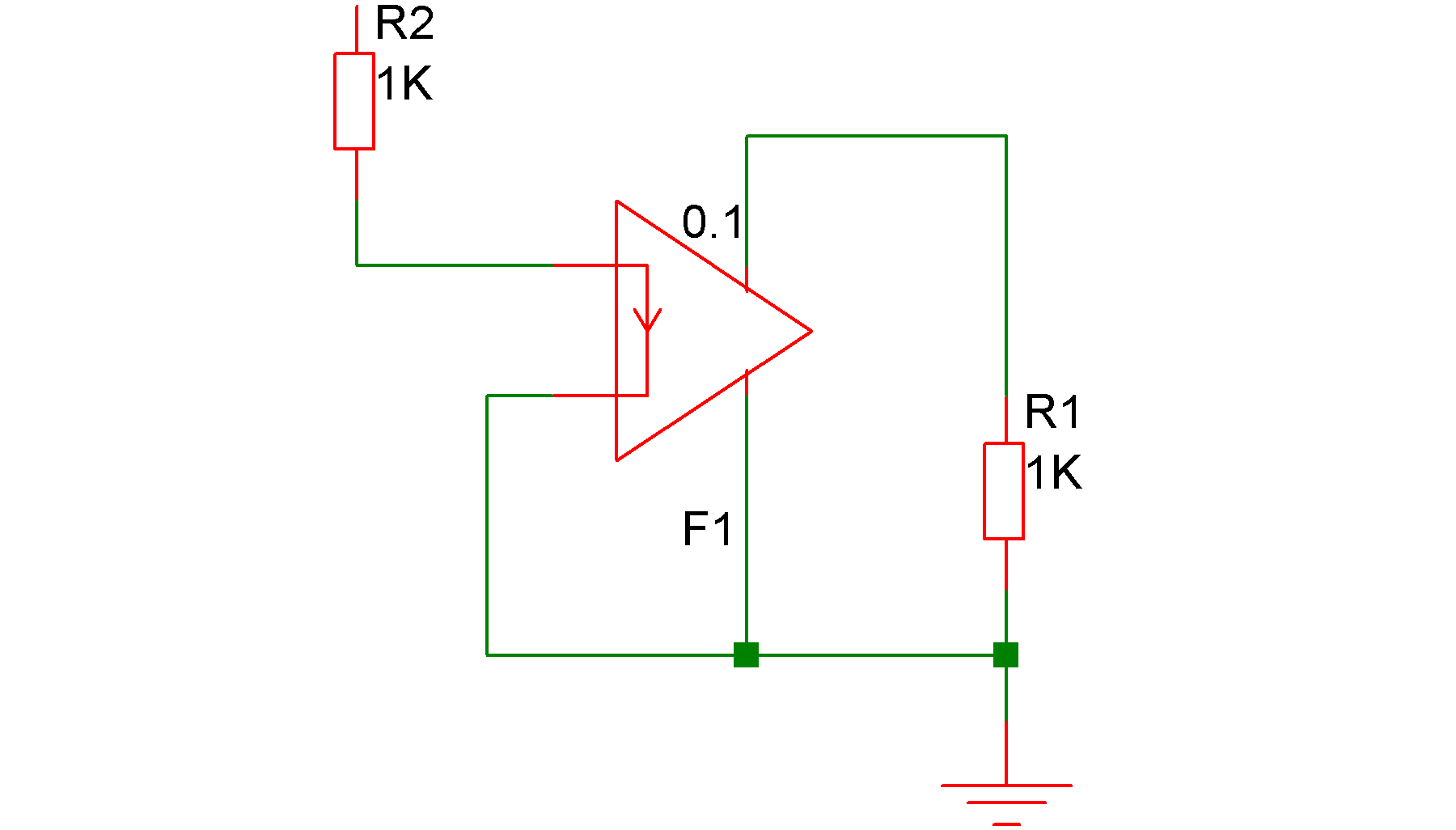
In the above circuit, the current in the output of F1 (flowing from top to bottom) will be 0.1 times the current in R2.

Polynomial Specification

The following is an extract from the SPICE2G.6 user manual explaining polynomial sources.

SPICE allows circuits to contain dependent sources characterised by any of the four equations

  • i=f(v)
  • v=f(v)
  • i=f(i)
  • v=f(i)

where the functions must be polynomials, and the arguments may be multidimensional. The polynomial functions are specified by a set of coefficients p0, p1, ..., pn. Both the number of dimensions and the number of coefficients are arbitrary. The meaning of the coefficients depends upon the dimension of the polynomial, as shown in the following examples:

Suppose that the function is one-dimensional (that is, a function of one argument). Then the function value fv is determined by the following expression in fa (the function argument):

\[ fv = p0 + (p1.fa) + (p2.fa^2) + (p3.fa^3) + (p4.fa^4) + (p5.fa^5) + ... \]

Suppose now that the function is two-dimensional, with arguments fa and fb. Then the function value fv is determined by the following expression:

\[ \begin{split} fv = p0 + (p1.fa) + (p2.fb) + (p3.fa^2) + (p4.fa.fb) + (p5.fb^2) \\ + (p6.fa^3) + (p7.fa^2.fb) + (p8.fa.fb^2) + (p9.fb^3) + ... \end{split} \]

Consider now the case of a three-dimensional polynomial function with arguments fa, fb, and fc. Then the function value fv is determined by the following expression:

\[ \begin{split} fv = p0 + (p1.fa) + (p2.fb) + (p3.fc) + (p4.fa^2) + (p5.fa.fb) + (p6.fa.fc) + (p7.fb^2) + (p8.fb.fc) \\ + (p9.fc^2) + (p10.fa^3) + (p11.fa^2.fb) + (p12.fa^2.fc) + (p13.fa.fb^2) + (p14.fa.fb.fc) \\ + (p15.fa.fc^2) + (p16.fb^3) + (p17.fb^2.fc) + (p18.fb.fc^2) + (p19.fc^3) + (p20.fa^4) + ... \end{split} \]

Note If the polynomial is one-dimensional and exactly one coefficient is specified, then SPICE assumes it to be p1 (and p0 = 0.0), in order to facilitate the input of linear controlled sources.

◄ Capacitor   Current Controlled Voltage Source ▶