Continuous or Discrete Time Filter

The Continuous or Discrete Time Filter models either a continuous time filter or a discrete time filter, with a parameter editing dialog which calculates the coefficients. You can enter the coefficients for a s-domain or z-domain transfer function and the dialog will calculate an equivalent filter in the other domain using one of the three mapping functions.

These filters are available in 1st and 2nd order, as the models used for the discrete time filter are limited to the second order. Higher order filters can be realized by cascading two or more filters.

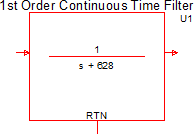
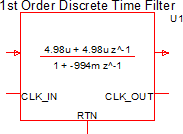
The electrical model used for these filters is either the Laplace Filters (1st, 2nd, 3rd Order) for a continuous time implementation, and for the discrete time implementation, the 1st Order Discrete Time Filter or 2nd Order Discrete Time Filter, depending on the filter order. The difference between this part and the Laplace and Discrete Time filters is the calculator dialog.

In this topic:

Model Name: Continuous or Discrete Time Filter
Simulator: This device is compatible with the SIMPLIS simulator.
Parts Selector Menu Locations:
  • Analog Functions > Laplace Transfer Functions > Continuous or Discrete Time Filter (Version 8.1+)
  • Digital Functions > Discrete Time Filters > Continuous or Discrete Time Filter (Version 8.1+)
Symbol Library: simplis.sxslb
Model File:
  • simplis_analog_functions.lb
  • simplis_discrete_time_filters.lb
Subcircuit Names: SIMPLIS_CONT_OR_DISCRETE_TIME_FILTER
Symbols:
 
Multiple Selections: Multiple devices can be selected and edited simultaneously.

Converting a Continuous Time (s-domain) Transfer Function to the Z-Domain

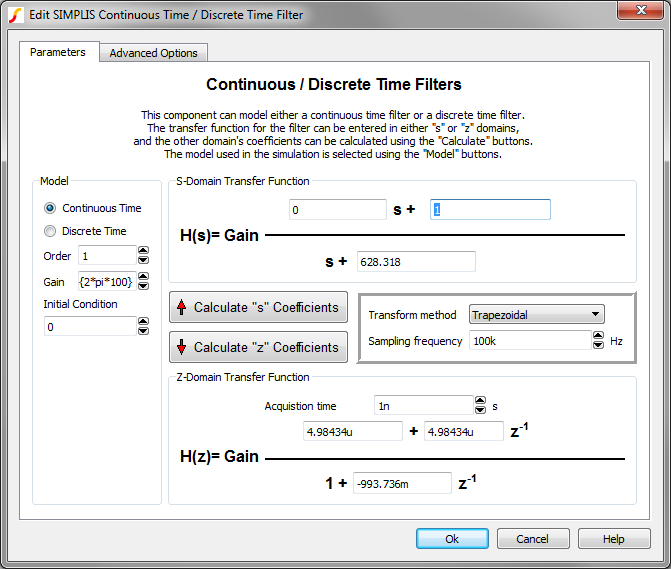
The filter has a calculator dialog which converts an s-domain transfer function to the z-domain or vice versa. This section assumes you have a s-domain transfer function which you would like to convert to the z-domain. To convert a z-domain transfer function to the s-domain, see Converting a Discrete Time (z-domain) Transfer Function to the S-Domain.

To configure the Continuous or Discrete Time Filter as a discrete-time filter, follow these steps:

  1. Double click the symbol on the schematic to open the editing dialog.
  2. On the editing dialog:
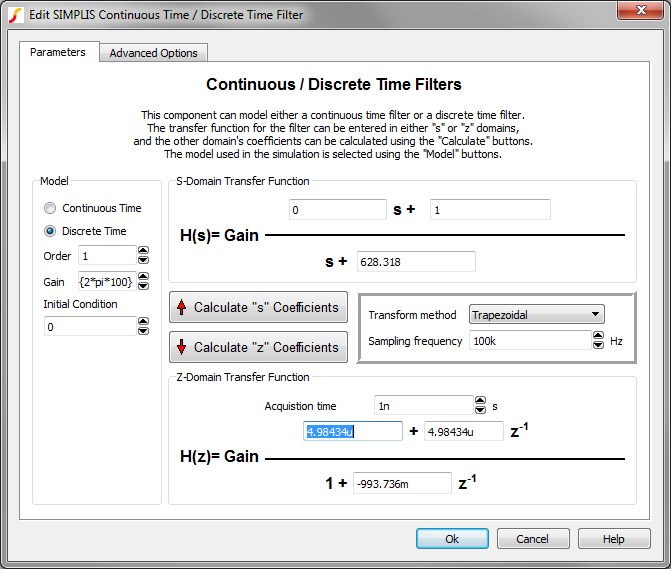
    1. Select the Discrete Time radio button.
    2. Select your desired filter order using the Order parameter.
      Result: The transfer functions to the right of the Order control are updated to reflect the current filter order.
    3. Enter the coefficients for your S-Domain Transfer Function for which you wish to calculate an equivalent z-domain transfer function.
    4. Enter your Sampling frequency and select your desired Transform method.
    5. Click the Calculate "z" Coefficients button.
      Result: The Z Domain Transfer Function coefficients are updated with values calculated from the S-Domain Transfer Function coefficients.
    6. Click Ok.
      Result: The symbol on the schematic changes to a discrete time filter with input and output clock pins, and the equation is updated on the symbol. If multiple filters were selected, each filter symbol is replaced and each filter is identical.

Converting a Discrete Time (z-domain) Transfer Function to the S-Domain

The filter has a calculator dialog which converts an s-domain transfer function to the z-domain or vice versa. This section assumes you have a z-domain transfer function which you would like to convert to the s-domain. To convert a s-domain transfer function to the z-domain, see Converting a Continuous Time (s-domain) Transfer Function to the Z-Domain.

To configure the Continuous or Discrete Time Filter as a continuous-time filter, follow these steps:

  1. Double click the symbol on the schematic to open the editing dialog.
  2. On the editing dialog:
    1. Select the Continuous Time radio button.
    2. Select your desired filter order using the Order parameter.
      Result: The transfer functions to the right of the Order control are updated to reflect the current filter order.
    3. Enter the coefficients for your Z-Domain Transfer Function for which you wish to calculate an equivalent z-domain transfer function.
    4. Enter your Sampling frequency and select your desired Transform method.
    5. Click the Calculate "s" Coefficients button.
      Result: The S Domain Transfer Function coefficients are updated with values calculated from the Z-Domain Transfer Function coefficients.
    6. Click Ok.
      Result: The symbol on the schematic changes to a continuous time filter and the equation is updated on the symbol. If multiple filters were selected, each filter symbol is replaced and each filter is identical.

Parameter Editing Controls

The main parameter editing controls are described in the table below.

Parameter Groupings/Labels Units Description
S-Domain Transfer Function   Enter the S-Domain filter coefficients in the text boxes. When you change the Order parameter, the equation and the available text boxes will change accordingly. Parameterized values using {} expressions are not permitted for these parameters.
Z-Domain Transfer Function   Enter the Z-Domain filter coefficients in the text boxes. When you change the Order parameter, the equation and the available text boxes will change accordingly. Parameterized values using {} expressions are not permitted for these parameters.
Calculate "s" Coefficients   This button uses the Z-Domain Transfer Function parameters, the Transform method, and the Sampling frequency to calculate an equivalent s-domain filter.
Calculate "z" Coefficients   This button uses the S-Domain Transfer Function parameters, the Transform method, and the Sampling frequency to calculate an equivalent z-domain filter.
Transform method   The transform method
Sampling frequency   The sampling frequency for the discrete time filter. This is used to calculate both the s-domain and z-domain coefficients. Parameterized values using {} expressions are not permitted for this parameter
Order   The filter order. Parameterized values using {} expressions are not permitted for this parameter
Gain   The filter gain
Initial Condition - IC V Initial output voltage of the filter

The dialog has an Advanced Options tab with three controls which affect the precision of the model and the transfer function displayed on the symbol. There are text descriptions on the dialog tab to the right of each control which describe the control's function.

Previous Version Compatibility

The subcircuit and editing dialog for the Continuous/Discrete Time filter were introduced in version 8.10. The filter will not simulate nor will it be editable in versions prior to 8.10.

For continuous time filters which are compatible with previous versions, see the part selector locations:
  • Analog Functions > Laplace Transfer Functions > 1st-order Laplace Transfer Function
  • Analog Functions > Laplace Transfer Functions > 2nd-order Laplace Transfer Function

For discrete time filters which are compatible with previous versions, see the part selector locations:

  • Obsolete > Digital Functions > 1st Order Discrete Time Filter (Obsolete)
  • Obsolete > Digital Functions > 2nd Order Discrete Time Filter (Obsolete)

Examples

Below are two examples of varying complexity which demonstrate how to use the Continuous/Discrete Time filters.

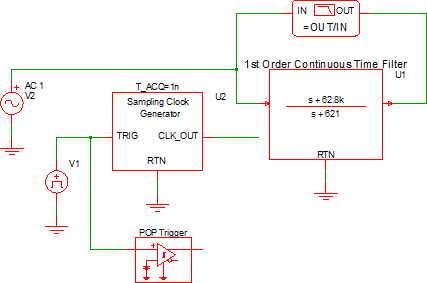
Example - Simple 1st Order Filter with One Pole and One Zero

The test circuits used to generate the waveform examples in the next section can be downloaded here:
simplis_081_continuous_time_pole_zero.sxsch simplis_081_discrete_time_pole_zero.sxsch

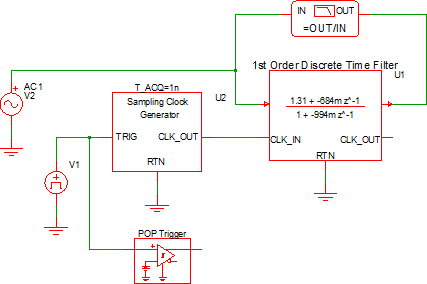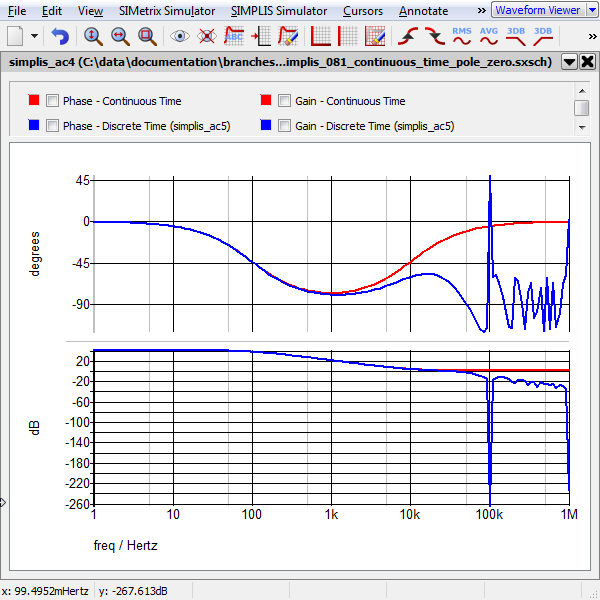
Waveforms - Simple 1st Order Filter with One Pole and One Zero

The schematics are configured to output the gain/phase waveforms to the same grid so the two filters can be easily compared. The AC response for the two filters is shown below:

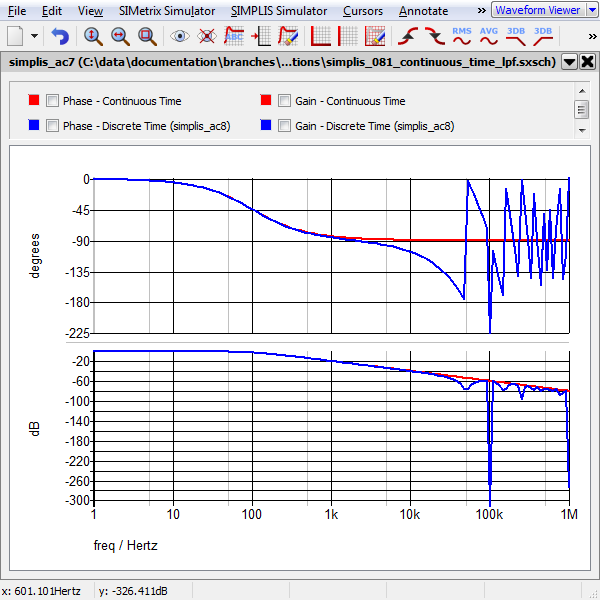
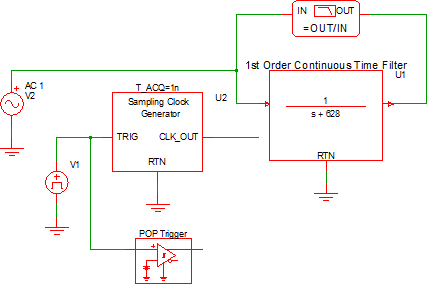
Example - 1st Order Low Pass Filter (LPF)

The test circuits used to generate the waveform examples in the next section can be downloaded here:
simplis_081_continuous_time_lpf.sxsch simplis_081_discrete_time_lpf.sxsch

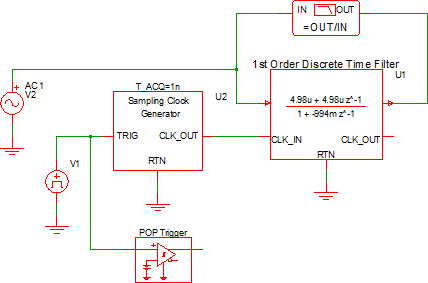Waveforms - 1st Order Low Pass Filter (LPF)

The schematics are configured to output the gain/phase waveforms to the same grid so the two filters can be easily compared. The AC response for the two low pass filters is shown below: